Welcome to the Grid: The LA Bus System

The bus system in Los Angeles covers practically the whole city if one knows how to take them. Los Angeles is a place where I don't really mind not having a car. I probably wouldn't use it that much even if I do have one. You'll be surprised of all the places you can go without a car. There are ways to get up to the Griffith Observatory and the Getty Villa in Malibu. Find out how below.

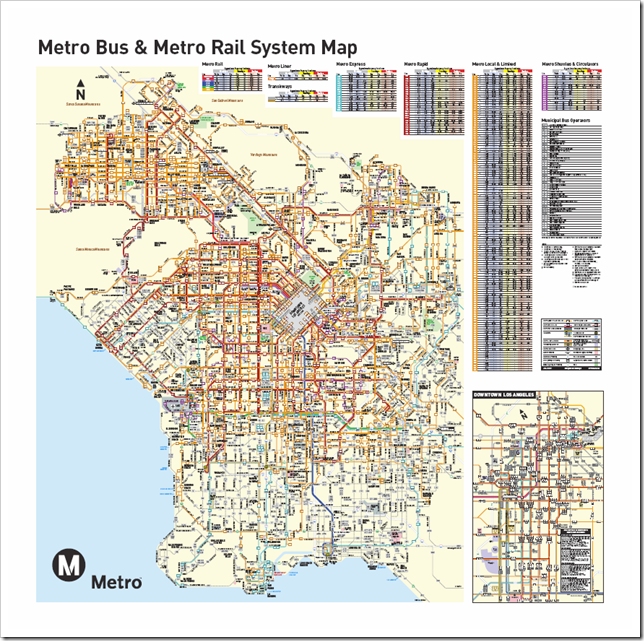
There are several different bus companies. I take the Big Blue Bus when going to the shores, everywhere else, the LA Metro. When I first got here, Google Map was not as updated as it is now. It missed a lot of bus lines, and showed only the line number without specifying which bus system it is showing (If I'm new around here, how can I know if it's Metro line 2 or BBB line 2 that I'm suppose to take?). Sometimes I get "no transportation possible" for my queries even though I know buses run along my destination (I was trying to get to the Greystone Mansion then). So I got myself a few copies of bus system maps. You can see what they look like below. Wasn't it a headache to read!

Thankfully, Google Map now offers pretty accurate and detailed information on public transportation. Even the ones that were previously missing were replaced. This is how you get to the Griffith Observatory: on weekends, as shown on Google Map:

Vermont/ Sunset Station

DASH Weekend Observatory Shuttle Bus

It will take you all the way up to the observatory. Neat! I didn't know that when I first got here. There was so few information. I settled to tagging along whenever someone with a car was going that way, else I'm well prepared to hike the rest of the way up there (which probably isn't a good idea). I'm only too glad to be spared the pain now with Google's help. As a bonus, the time shown on Google is pretty accurate. It's perfect for trip planning now.

OK, more on the bus systems:

The Metro system includes bus lines as well as rail lines. Regular bus fares are $1.50 per ride, and rail lines only accept TAP cards, which can be used to board buses as well. Consider buying a TAP card if you're making transfers to your destination. You can get them at local supermarkets or TVMs. It's one buck for the card and 5 dollars for a day pass. Credit can be added online, at TVMs, or on the bus. Simple! Plus, there'll be no need to worry about collecting coins anymore.

The Big Blue Bus and Clover City Bus covers the Santa Monica area, and Clover City, respectively. Regular bus fare is one dollar per ride. I highly recommend going to the beaches by bus. Parking space is hard to find, the price for fuel and parking combined far exceeds that of public transportation, and you'll be doing a favor to the Earth.

Lastly, here are the detailed bus fares for the two public transportation systems: LA Metro, Big Blue Bus. Happy Riding!

Easy Reading: Fortunately, the Milk

TGIF! What a nice day it was to go down to the Los Angeles Public Library and get some easy reading material. I heard about Fortunately, the Milk from Neil Gaiman's Tumblr (Nice marketing, Mr. Gaiman!), and had wanted to get my hands on one ever since its publication last month. Imagine my excitement when I found out that the library already have several copies and I can place a hold for one (They circulate fast and were all checked out.). Now imagine what it's like to finally get a message after a week's waiting:

The following item(s) you requested are being held for you:
Gaiman, Neil.
Fortunately, the milk /
The item will be held until: 11/04/2013

It was heavenly! Skipping down the streets with my headphone on, I couldn't be sure if the silly grin was due to the giddiness of knowing what I was about to pick up or the cheerful audio book playing on my headphones (The book was Chitty Chitty Bang Bang narrated by David Tennant.) was simply too much fun.

With all these excitement, I finished the book in no time. And I am happy to say, it absolutely lived up to my expectations. The story was most curious. 10 years ago I would find it fantastic. Now, nearly an adult, I find it cute and silly. I nearly forgot how good it is to read adventure stories without having to feel anxious about the characters. Another great element of children's books are the illustrations. How I adore them! People with curly fingers, animals standing on their hind legs, strange creatures with big eyes.... Fortunately, the Milk has become one of my all time favorite children's books. It is something I would love to share with my younger cousins and probably read to them when I have the chance.

* * *

Note: This was originally from my other blog: College Frenzy. Realizing that the contents actually gave some insight of what my life in LA is like, I decided to repost it here (with a few adjustments).

City of Angels: First Impressions

It is easy to forget just how big United States is. Even today, with the frequent communication and transportation, the differences between states can still be surprising. I remembered United States as the harbor city of New England: cool breeze, seagulls, stone-paved streets, neat little cafes, and people in long coats. Walking down the streets of LA on my first week was the strangest of experiences: Everyone was in sandals, short jeans and sunglasses; People talk in all kinds of languages; The hills were bare except for palm trees and bushes; And there were more sports cars on the road than I've ever seen. There was no trace of the romantic European feel that I was expecting. I was, to be honest, slightly disappointed.

Today, however, if anyone asks, I am in love with this city.

LA is like the ocean. She seems flat and unchanging on the surface, but underneath, she is full of life, beauty and unknown adventures. One just needs the right gears and some time to explore. Visiting any one museum or art gallery can take up a day. I've spend my time in art galleries and museums, seen some of the most famous masterpieces in the world, and many more expressive contemporary artworks. Whether it was the overall atmosphere or the inspiration from these experiences, I found myself taking up drawing even when I had abandoned the paint and brushes for many years. The city is also filled of history, even though the west coast was developed much later than other parts of the US. From  Felipe de Neve[1] to the Mexican-American War[2] to the rise of the film industry[3], a trip to the Natural History Museum can only tell so much of all the fascinating stories.

On a more practical note, one can live in LA without a car. Isn't it great? There are places to shop and dine within walking distance. If one is picky and wish to go to specific places that happened to be farther away, there is always the bus. Bus lines are spread out like thick spider webs here and most of them come and go fairly frequently. For those that are unfamiliar with the system and need to look up what bus(s) to take, however, it may be slightly confusing. Google Maps only shows a fraction of the bus lines and does not specify which buses belong to the Metro System and which belong to the Big Blue Bus or Culver City Bus System. For bus info and how to look for bus schedule in LA, see this post here. Once you get your head around the system, however, it can be more convenient than driving around town. No need to worry about parking spaces and gasoline prices!

Steadily, as the city became more familiar, and the initial shock passed, I felt like this is the city to stay in. The weather is perfect, getting around is convenient, and there are plenty to do year-round. My todo list is infinitely long and growing! Browsing through all the theatre productions and music festivals happening around town, it all came down to the same problem: Either I don't have time to go to the cheap/free events, or the pricey tickets put too much financial pressure for a jobless student. So much is going on all the time that instead of feeling bored, one worries about missing all the excitement!

Catching Up With Adventures

It has been 84 days since I first touched down on the sunny city of Los Angeles. This was not for a holiday trip. Soon, there will be serious studying to do. Admittedly, it was too early to come in for academic purposes: School would not start until mid-September. However, due to a naturally anxious personality, I had to see myself properly settled down. The result? Plenty of time to kill.

Los Angeles is a big city. It has more museums per capita than any other city in the world. To be exact, there are 841 museums and art galleries combined in Los Angeles County[1]. Her busy streets are easily navigable using public transit (Although with the various bus lines, it may seem confusing at first. More on the subject in later posts). Within a month, I have visited most of the tourist attractions and some of the lesser known paradise. Much excitement kept me fairly occupied and until now, I have neglected to sort out all the photographs (Did I mention that LA is a photographer's heaven?), notes and journals. In the coming weeks I plan to get everything up here, and hopefully provide some useful information (perhaps exclusively for students traveling on budget).

To get things started, here are a list of topics I'll try to cover. Once relevant posts are updated, there will be a link to each post/story/info.

• City of Angels: First Impressions
• Traveling on foot
• LA Public Transportation
• At the train station

• The Getty Museum(s)
• Santa Monica Beach and nearby regions
• Venice Beach \ Boardwalk
• The Grove: traveling alone
• The Venice Canals
• Navigating the hills of UCLA
• Greystone Mansion: forgotten glory
• Adventures on Rodeo Drive: more than window shopping
• From Sunset Boulevard to Hollywood
• Downtown LA (in parts)
• Space Shuttle Endeavor
• Universal Studios
• Nerdy Pleasures Libraries

* * *

References

1. "The Los Angeles Region". Loyola Marymount University. May 5, 2008. Retrieved 2013-10-23.

The Newton-Raphson Method

This post was originally on my other blog College Franzy, which is dedicated entirely to sorting out the notes and studies I've done during college. This particular subject, the Newton-Raphson method has always been very helpful to me. So frequent did I find myself searching through my notes that they would soon fall apart if they are not stored somewhere more permanent. So I set down one day and posted Newton-Raphson Method: Application. I am so very proud of it that, very soon, I realized that I have to share it here as well. The following is the full content of the original post. Enjoy!

* * *

This is an application of the Newton-Raphson method for finding the joint angles of a mechanism. This was adapted from a note I made in a class called Mechanics of Machines in my sophomore year. It has proven useful to me for numerous times since then. The Newton-Raphson method can be used on any closed-loop mechanisms, including non-inverted and inverted slider-crank mechanisms. It also converges relatively fast in many common cases which makes it such a convenient tool. Throughout the years the Newton-Raphson method one of my favorite tools as a ME student. 

--

Consider the double-loop mechanism:

Link 1 is the input, i.e. the rotation angle of link 1 is specified. Since this mechanism have one degree of freedom the positions of all other links can be found. Realizing that the two loops shown in the figure are in fact two four-bar linkages, we can solve them independently.

First of all, to find the joint angles of the 4-bar linkage made by links 1, 2, 3, and the ground link,notice that the vectors R₁, R₂, R₃, and R₆' have the following relationships:

$R_1+R_2-R_3-R_6=0$.

This is the loop equation for Loop 1. One must be aware of the direction of the vectors. Rewriting this equation in terms of link lengths r₁, r₂, r₃, r₆', and joint angles $\theta_1,\ \theta_2,\ \theta_3,$ and $\phi_6'$, it becomes:

$r_1\cos\theta_1+r_2\cos\theta_2-r_3\cos\theta_3-r_6\cos\phi_6=0$ $r_1\sin\theta_1+r_2\sin\theta_2-r_3\sin\theta_3-r_6\sin\phi_6=0$.

There are two unknowns, $\theta2$ and $\theta3$. The goal here is to find solutions to these two equations:

$F_1(\theta_2,\ \theta_3)=r_1\cos\theta_1+r_2\cos\theta_2-r_3\cos\theta_3-r_6\cos\phi_6$ $F_2(\theta_2,\ \theta_3)=r_1\sin\theta_1+r_2\sin\theta_2-r_3\sin\theta_3-r_6\sin\phi_6$

Here we will apply the Newton-Raphson method.

• Find estimated values $\theta_2$ and $\theta_3$. Let's call them $\theta_2'$ and $\theta_3'$.
• The partial differivative of F1 and F2 with respect to $\theta1$ and $\theta2$ are
$\frac{\partial F_1}{\partial \theta_2}=-r_2\sin\theta_2$,    $\frac{\partial F_1}{\partial \theta_3}=r_3\sin\theta_3$

$\frac{\partial F_2}{\partial \theta_2}=r_2\cos\theta_2$,   $\frac{\partial F_2}{\partial \theta_2}=-r_3\cos\theta_3$.



Since the values are estimated, it is highly unlikely that they will be the exact solution to F1 and F2. That is, F1 and F2 will not be zero when substituting these values into the equations. We write:

$F_1(\theta_2',\ \theta_3')=\epsilon_1'$ and $F_2(\theta_2',\ \theta_3')=\epsilon_2'$.
Then Newton-Raphson method yields that

$-r_2\sin\theta2'\times(\Delta\theta_2)+r_3\sin\theta_3\times(\Delta\theta_3)=\epsilon_1-\epsilon_1'$
$r_2\cos\theta2'\times(\Delta\theta_2)-r_3\cos\theta_3\times(\Delta\theta_3)=\epsilon_2-\epsilon_2'$where $\epsilon_1=\epsilon_2=0$ in this case (the cost of F1 and F2).
Solving the equations in 4. gives the change for $\theta_2$ and $\theta_3$.

.
The new estimation for the two values are $\theta_2''=\theta_2'+\Delta\theta_2$ and $\theta_3''=\theta_3'+\Delta\theta_3$, respectively. Using these new values we can start the process from step 3 and find new values again. The values will converge to the exact value of  $\theta_2$ and $\theta_3$. Once the values are withing tolerance, the procedure is terminated and we had our answer.

The procedure for Loop 2 is the same as that described above. Just use the Newton-Raphason method again to find  $\theta_4$ and $\theta_5$.