This post was originally on my other blog College Franzy, which is dedicated entirely to sorting out the notes and studies I've done during college. This particular subject, the Newton-Raphson method has always been very helpful to me. So frequent did I find myself searching through my notes that they would soon fall apart if they are not stored somewhere more permanent. So I set down one day and posted Newton-Raphson Method: Application. I am so very proud of it that, very soon, I realized that I have to share it here as well. The following is the full content of the original post. Enjoy!
* * *
This is an application of the Newton-Raphson method for finding the joint angles of a mechanism. This was adapted from a note I made in a class called Mechanics of Machines in my sophomore year. It has proven useful to me for numerous times since then. The Newton-Raphson method can be used on any closed-loop mechanisms, including non-inverted and inverted slider-crank mechanisms. It also converges relatively fast in many common cases which makes it such a convenient tool. Throughout the years the Newton-Raphson method one of my favorite tools as a ME student.
--
Consider the double-loop mechanism:
Link 1 is the input, i.e. the rotation angle of link 1 is specified. Since this mechanism have one degree of freedom the positions of all other links can be found. Realizing that the two loops shown in the figure are in fact two four-bar linkages, we can solve them independently.
First of all, to find the joint angles of the 4-bar linkage made by links 1, 2, 3, and the ground link,notice that the vectors R1, R2, R3, and R6' have the following relationships:
$R_1+R_2-R_3-R_6=0$.
This is the loop equation for Loop 1. One must be aware of the direction of the vectors. Rewriting this equation in terms of link lengths r1, r2, r3, r6', and joint angles $\theta_1,\ \theta_2,\ \theta_3,$ and $\phi_6'$, it becomes:
$r_1\cos\theta_1+r_2\cos\theta_2-r_3\cos\theta_3-r_6\cos\phi_6=0$
$r_1\sin\theta_1+r_2\sin\theta_2-r_3\sin\theta_3-r_6\sin\phi_6=0$.
$F_1(\theta_2,\ \theta_3)=r_1\cos\theta_1+r_2\cos\theta_2-r_3\cos\theta_3-r_6\cos\phi_6$
$F_2(\theta_2,\ \theta_3)=r_1\sin\theta_1+r_2\sin\theta_2-r_3\sin\theta_3-r_6\sin\phi_6$
Here we will apply the Newton-Raphson method.
- Find estimated values $\theta_2$ and $\theta_3$. Let's call them $\theta_2'$ and $\theta_3'$.
- The partial differivative of F1 and F2 with respect to $\theta1$ and $\theta2$ are
- Since the values are estimated, it is highly unlikely that they will be the exact solution to F1 and F2. That is, F1 and F2 will not be zero when substituting these values into the equations. We write:$F_1(\theta_2',\ \theta_3')=\epsilon_1'$ and $F_2(\theta_2',\ \theta_3')=\epsilon_2'$.
- Then Newton-Raphson method yields that$-r_2\sin\theta2'\times(\Delta\theta_2)+r_3\sin\theta_3\times(\Delta\theta_3)=\epsilon_1-\epsilon_1'$$r_2\cos\theta2'\times(\Delta\theta_2)-r_3\cos\theta_3\times(\Delta\theta_3)=\epsilon_2-\epsilon_2'$where $\epsilon_1=\epsilon_2=0$ in this case (the cost of F1 and F2).
- Solving the equations in 4. gives the change for $\theta_2$ and $\theta_3$.
- The new estimation for the two values are $\theta_2''=\theta_2'+\Delta\theta_2$ and $\theta_3''=\theta_3'+\Delta\theta_3$, respectively. Using these new values we can start the process from step 3 and find new values again. The values will converge to the exact value of $\theta_2$ and $\theta_3$. Once the values are withing tolerance, the procedure is terminated and we had our answer.
$\frac{\partial F_1}{\partial \theta_2}=-r_2\sin\theta_2$, $\frac{\partial F_1}{\partial \theta_3}=r_3\sin\theta_3$
$\frac{\partial F_2}{\partial \theta_2}=r_2\cos\theta_2$, $\frac{\partial F_2}{\partial \theta_2}=-r_3\cos\theta_3$.
$\frac{\partial F_2}{\partial \theta_2}=r_2\cos\theta_2$, $\frac{\partial F_2}{\partial \theta_2}=-r_3\cos\theta_3$.

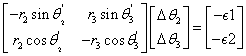
No comments:
Post a Comment